Emitter Identification
Est. read time: 1 minute | Last updated: February 16, 2026 by John Gentile
Contents
import numpy as np
import matplotlib.pyplot as plt
from rfproto import impairments, plot, sig_gen
import plotly.graph_objects as go
import plotly.io as pio
pio.renderers.default = "png" # "notebook_connected"
fs = 10e6
num_chirp_samples = 2000
upchirp = sig_gen.cmplx_dt_lfm_chirp(2.0, 2e6, 3e6, fs, num_chirp_samples)
plt.specgram(upchirp, pad_to=1024, Fs=fs)
plt.xlabel('Time (s)')
plt.ylabel('Frequency (Hz)')
plt.show()
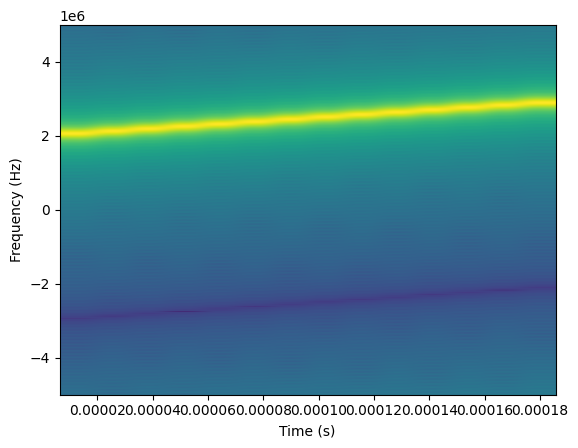
pulse_plus_noise = impairments.awgn(1.0, 5 * num_chirp_samples)
pulse_plus_noise[3000:5000] += upchirp
plt.specgram(pulse_plus_noise, pad_to=1024, Fs=fs)
plt.xlabel('Time (s)')
plt.ylabel('Frequency (Hz)')
plt.show()
Time Difference of Arrival (TDOA)
# Define parameters
c = 1.0 # Speed of signal (arbitrary units for simulation)
#R = np.array([[0, -1], [12, 0], [0, 11], [14, 13]]) # Receiver positions in 2D
R = np.array([[0, -1], [12, 0], [14, 13]]) # Receiver positions in 2D
S_true = np.array([5, 5]) # True source position
sigma = 0.5 # Noise standard deviation for time differences
# Simulate true time differences with noise
distances = np.linalg.norm(R - S_true, axis=1) # Euclidean distances to source
t = distances / c # True time of arrivals
delta_t_true = t[1:] - t[0] # Time differences relative to first receiver
delta_t_measured = delta_t_true + np.random.normal(0, sigma, size=delta_t_true.shape)
# Create a grid for source position candidates
x = np.arange(-5, 15, 0.1) # X range
y = np.arange(-5, 15, 0.1) # Y range
X, Y = np.meshgrid(x, y) # 2D grid
# Compute cost function over the grid
R0 = R[0] # Reference receiver
d0 = np.sqrt((X - R0[0])**2 + (Y - R0[1])**2) # Distance to reference receiver
cost = np.zeros_like(X) # Initialize cost array
for i in range(1, len(R)):
Ri = R[i]
di = np.sqrt((X - Ri[0])**2 + (Y - Ri[1])**2) # Distance to receiver i
delta_t_pred = (di - d0) / c # Predicted time difference
e = delta_t_measured[i-1] - delta_t_pred # Error
cost += e**2 # Sum of squared errors
# Estimate source position
min_idx = np.unravel_index(np.argmin(cost), cost.shape) # Index of minimum cost
S_est = [X[min_idx], Y[min_idx]] # Estimated source position
# Plot the localization heatmap with receivers and bearing lines
plt.figure(figsize=(8, 6))
plt.pcolormesh(X, Y, np.log(cost + 1), cmap='hot') # Log scale for better visualization
plt.colorbar(label='Log(Cost + 1)')
plt.scatter(S_true[0], S_true[1], c='blue', label='True Source', edgecolors='k')
plt.scatter(S_est[0], S_est[1], c='red', label='Estimated Source', edgecolors='k')
plt.scatter(R[:, 0], R[:, 1], c='green', label='Receivers', edgecolors='k', s=100)
for i, receiver in enumerate(R):
plt.plot([receiver[0], S_est[0]], [receiver[1], S_est[1]], 'b--',
label='Bearing Lines' if i == 0 else None) # Label only first line
plt.legend()
plt.xlabel('X')
plt.ylabel('Y')
plt.title('TDOA Localization Heatmap with Receivers and Bearing Lines')
plt.axis('equal')
plt.show()
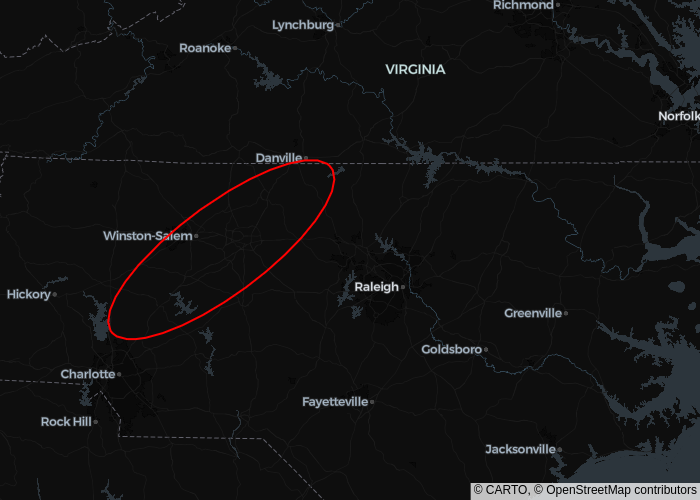
Geolocation
def ellipse(x_center=0, y_center=0, angle=0.0, a=1, b=1, N=100):
angle = np.deg2rad(angle)
ax1 = [np.cos(angle), np.sin(angle)]
ax2 = [-np.sin(angle), np.cos(angle)]
t = np.linspace(0, 2*np.pi, N)
xs = a * np.cos(t)
ys = b * np.sin(t)
R = np.array([ax1, ax2]).T
xp, yp = np.dot(R, [xs, ys])
x = xp + x_center
y = yp + y_center
return x, y
fig = go.Figure(go.Scattermap(mode="markers"))
fig.update_layout(
margin={'r':0,'t':0,'l':0,'b':0},
map = {
'style': "dark",
'center': {'lon': -79, 'lat': 36 },
'zoom': 6.5
},
)
x_center = -80 # Example longitude
y_center = 36 # Example latitude
a = 1 # Semi-major axis (in degrees of lat/lon, approximate)
b = 0.3 # Semi-minor axis (in degrees of lat/lon, approximate)
angle = 30 # Rotation angle
x, y = ellipse(x_center, y_center, angle, a, b)
fig.add_trace(go.Scattermap(
mode="lines",
lon=x,
lat=y,
marker={'size': 10},
line={'color': 'red'}
))
fig.show()
References
- Emitter Detection and Geolocation for Electronic Warfare
- nodonoughue/emitter-detection-book (MATLAB) & nodonoughue/emitter-detection-python (Python)
- Joint TDOA, FDOA and PDOA Localization Approaches and Performance Analysis
- Object Tracking Using Time Difference of Arrival (TDOA) - Mathworks