Unknown BPSK Decode

Est. read time: 2 minutes | Posted: September 29, 2025 by John Gentile

I saw an interesting DSP challenge come up in r/DSP, DrSDR/BPSK-Decode, in which a .wav file is given and we are looking to demodulate and decode the signal to get an “Amazon gift card claim code”.

We are given the following information about it:

Waveform is BPSK I/Q file with frequency and phase offset applied.
Sampling frequency of $f_{s} = 48kHz$
40 samples per bit, 144 bits in waveform, so total samples = 40 * 144
Bit mapping: 0 = 0deg, I = 1 & Q = 0 , 1 = 180deg, I = -1 & Q = 0
18 characters in waveform, each char is 8 bits (ASCII), with MSB sent first
First 8 bits of message is 01000001 or A in 8-bit ASCII

import numpy as np
import matplotlib.pyplot as plt
from scipy.io import wavfile
from rfproto import plot

First lets read in the .wav file and verify the sampling frequency given in the file metadata.

fs, wav_data = wavfile.read("./BPSK_IQ_Fs48KHz.wav")
N = len(wav_data)
print(f"Read {N} samples with fs={fs}")

Read 5760 samples with fs=48000

input_iq = wav_data[:, 0] + 1j * wav_data[:, 1]
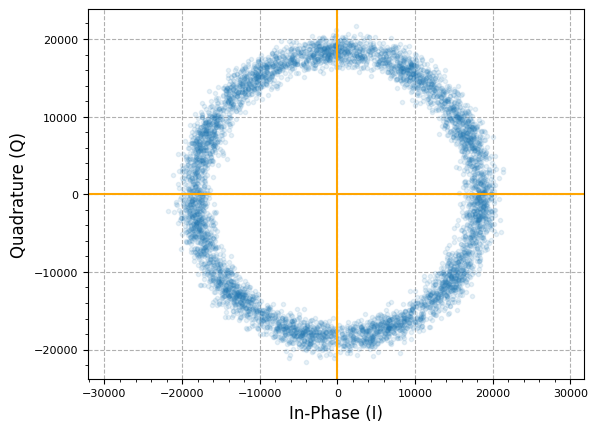
plot.IQ(input_iq, alpha=0.1)
plt.show()

png

Static (Non-Realtime) Demodulation

We can assume at first that both frequency and phase offsets are statically set in this synthetic case- thus, we can do some simplifications in both approaching each stage of compensation as full passes across the input data, as well in the type of processing to find and compensate for the given offsets towards carrier recovery.

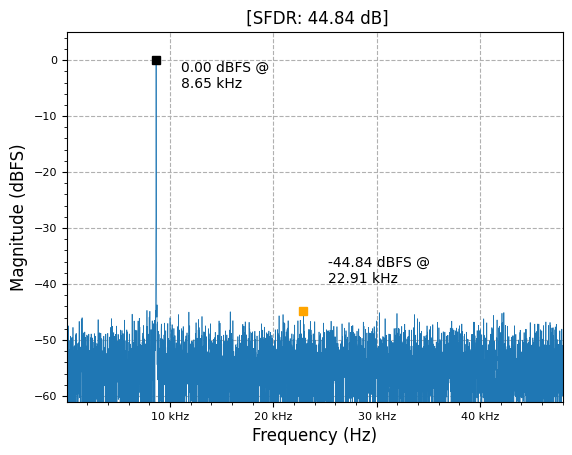
To find the frequency offset error, we can use the squaring trick which wipes off the modulation of a signal when raising to the power of the modulation-order (e.g. $x^{2}$ squaring for BPSK, $x^{4}$ for QPSK, etc.), which will then show a tone at double (or quadruple in the case of QPSK) when taking the FFT of the signal as the remaining frequency content is the offset of the double/quadrupled signal.

x2 = input_iq ** 2
plot.spec_an(x2, fs, scale_noise=True, norm=True)
plt.show()

png

freqs = np.fft.fftfreq(N, 1 / fs)
X2 = np.fft.fft(x2)

f_offset = freqs[np.argmax(np.abs(X2))] / 2.0
print(f"Frequency offset seen to be {f_offset} Hz")

Frequency offset seen to be 4320.833333333334 Hz

Now that the frequency offset is found, we can compensate for the rotation by multiplying the input signal by a negative frequency of that offset:

Y = x * e^{- j \omega t } = x * e^{- j 2 \pi f t }

t = np.arange(N) / fs
freq_corrected = input_iq * np.exp(-1j * 2 * np.pi * f_offset * t)
plot.IQ(freq_corrected, alpha=0.1)
plt.show()

png

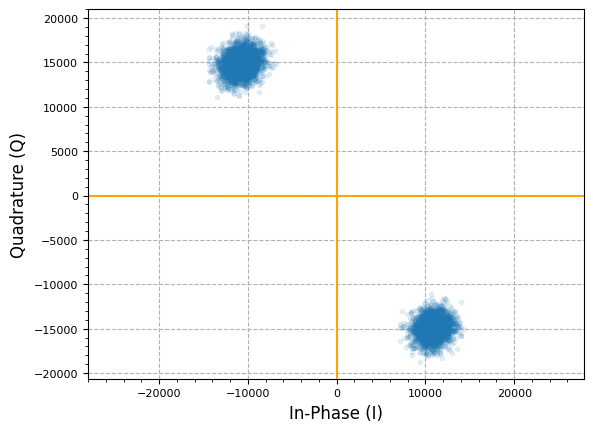
We can see that the BPSK constellation is now not rotating at all! However a phase offset is still seen- in the same way we used the squaring trick to remove the modulation to find the frequency offset, the same trick can be used to find the resultant phase offset (which would also be twice the phase offset of the underlying baseband signal). Here again we assume (and see above in the IQ plot) a static phase offset, so we take the average of all angles and apply the opposite phase correction using the phasor:

Y = x * e^{-j \theta}

x2 = freq_corrected ** 2
theta_avg = np.mean(np.angle(x2) / 2)
phase_corrected = freq_corrected * np.exp(-1j * theta_avg)

plot.IQ(phase_corrected, alpha = 0.1)
plt.show()

png

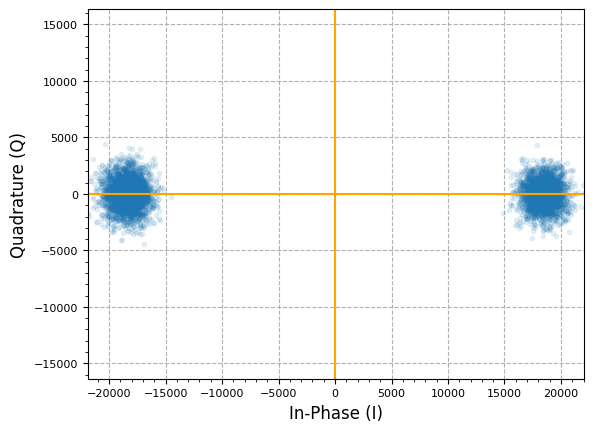
Now there’s no phase offset! As well, we can see in this IQ plot that the synthetically generated BPSK dataset has no timing offset, so we can go directly to decimating (downsampling) the data before taking hard-decisions to get output bits.

sps = 40 # Samples / symbol
decimated = phase_corrected[::sps]
plot.IQ(decimated, alpha = 0.4)
plt.show()

png

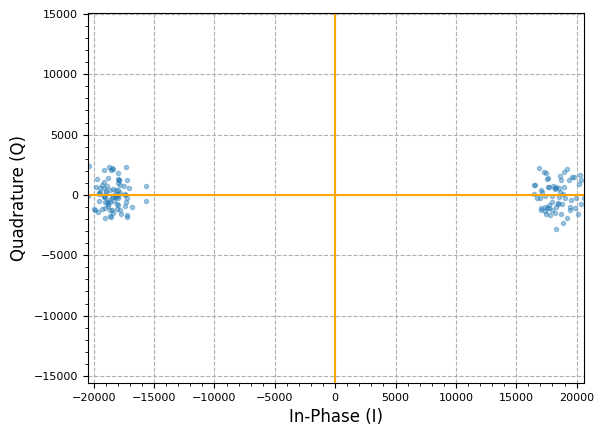
For hard-decision bits in BPSK, we can simply take the sign of the real portion:

bits = []
for sample in decimated:
    bit = 0 if sample.real > 0 else 1
    bits.append(bit)

Given the phase ambiguity of BPSK, we are given the first ASCII character is A- so if we don’t match that immediately, invert bits (or rotate phase in real-time system) to see if matching.

preamble = [0, 1, 0, 0, 0, 0, 0, 1]
if bits[:8] == preamble:
    print("Preamble found and matches expected, no inversion needed")
else:
    for i in range(len(bits)):
        bits[i] = 0 if bits[i] > 0 else 1
    if bits[:8] == preamble:
        print("Preamble found after inversion")
    else:
        print("Preamble not found!")

print(bits[:8])

Preamble found after inversion [0, 1, 0, 0, 0, 0, 0, 1]

message = ""
num_chars = 18
for i in range(num_chars):
    curr_bits = bits[i * 8 : (i+1) * 8]
    byte_str = ''.join(map(str, curr_bits))
    byte_val = int(byte_str, 2)
    message += chr(byte_val)

print(f"Final demodulated and decoded message: {message}")

Final demodulated and decoded message: ASLU-KZREUU-M9ZAW